May 10, 2016
Slider scaling
This is a (very, very, very1 delayed) response to an article on slider interfaes published last year by Baymard Institute. The article goes beyond what will be considered here — and you should read it.
Sliders are often used to give a visual cue in content filtering; the user drags a slider to a position corresponding to some value, and content is then filtered according to that value.
Linear slider scales provide a poor user experience, because the underlying data is rarely a uniform distribution. This creates two problems; large portions of the slider may represent no change in the filtering, and small portions may represent huge changes in the filtering. The article suggests solving these problems with the use of biased, logarithmic, or exponential scales. Real-world data often fits nicely on either a logarithmic or exponential curve, but not always. In fact, for any function we can come up with, there must exist a dataset that does not fit it! This means we cannot simply rely on linear, logarithmic, or exponential functions to save our day. In particular, we can not expect the same linear, logarithmic, or exponential function to fit all our data sets — we would generally have to tweak them to our use case. I propose the use of histogram equalization for creating biased scales — a custom mapping from slider-positions to values in the underlying data. In fact, I expect this solution to fit any dataset you might come up with.
Lenshawk lenses by focal length
Before I go further in-depth with the solution, let’s see an example. The two sliders below simulate filtering on the freely available Lens Hawk dataset, referenced in the Baymard article. For simplicity, instead of showing all the lenses that match the filter, the number of matches is displayed.
According to the article, Lens hawk uses an exponential scale for filtering on focal length. You can try it out here.
(Note: Their scale is 4-800, mine is 45-8000.)
Linear slider
Biased slider
We can immediately see that, at the middle of the slider, the linear scale matches 548/561 lenses (98%), where the biased scale matches 269/561 lenses (48%).
This means the right half of the linear-scale slider is used for only 2% of the items, while the remaining 98% is crammed into the left half. If you play with the sliders a little, you will notice that the linear scale puts nearly all of the lenses within the first ∼ 12% of the slider, while the biased scale distributes the lenses quite evenly.
So does the biased scale above provide a better user experience? While it seems like a vast improvement on the linear scale, it shifts the focus. On the linear scale, it is difficult to control the number of matching items, but on the biased scale, it is difficult to control the exact filter value!
If the relationship between the number of matched items and the filter value can be made apparent, the biased scale is a huge improvement. You may have noticed that on the biased scale, the filter value seems more jittery than the linear one. This is because I interpolate linearly between the positions that would actually change the filtering. For example, the filtering changes at value 170, and again at 180. Between those values, the filtering remains as if the slider was at 170. Because of the way I created the biased scale (more on that later), the easiest thing would be for me to display a filter value of 170 in that entire section of the slider. My guess is most people would find the resulting irregularity unintuitive, and be annoyed that they could not pick e.g. 174. Of course, this is just conjecture.
It might be that it is easy for people to see that, for a less-than-or-equal filter, the highest value lower than the wanted max matches the exact same items as the wanted max value — the only way to find out would be a user study, which is outside of both the scope of this post, and my comfort zone.
This is where the logarithmic or exponential scales are at an advantage; their smoothness seems to make them easier to use and understand, despite the non-linearity. Probably, a solution that weighs smoothness against scale utilization is possible2.
For now, let’s look at a method to create a biased scale for any data set, without the manual tweaking that logarithmic and exponential scales sometimes require.
Histogram Equalization
Recall that a slider-scale is simply a mapping from slider position to a threshold value for the underlying data. A biased scale is just such a mapping, tailored to your data. The properties we are looking for in this mapping are:
- Scale utilization; we wish to use the entire slider, not have all our data points clustered in a segment of the slider.
- Smoothness of distribution; we do not want the data to be clustered in small sections of the slider, making the slider overly sensitive. Accordingly, we do not want large sections of the slider that do not change the filtering.
As it turns out, these properties are valued in contrast adjustment as well.
A common problem in image processing is contrast adjustment. Contrast adjustment is used for example by photographers, for aesthetic purposes, and scientists have found use for it in image segmentation, which is used for things like computer vision and medical image analysis (If you’ve ever had an MRI, CT, or X-ray, the resulting images have likely been histogram-equalized).
Histogram equalization works for many types of data, but the canonical example is monochrome images. Pixels in a monochrome image can have values between the two extremes; black and white. But just like we didn’t have lenses with every possible focal length between 45 and 8000 in the Lenshawk example, you can have images that don’t utilize the space between black and white very well. It might be that there are no or few values in the brighter end of the spectrum (much like our Lenshawk example), or it might be that there are mostly very dark and bright values, but not much in between. Histogram equalization is used to assign new values to the image pixels, to better utilize the spectrum.
There is a direct correspondence between the problem of contrast adjustment, and our problem of slider scaling. In contrast adjustment, we want to maximize the use of the colour-range. In slider scaling, we want to maximize the use of our slider range — two seemingly equivalent problems.
There is an important difference between the two problems. In contrast adjustment we may (and will) change the actual colours in the image, but in slider scaling we may not adjust the values of the items we are filtering — if we are filtering products based on price, it would be problematic to change our prices to fit our slider. As it turns out, this is not a big problem — we don’t change the underlying values, just how our slider maps to them!
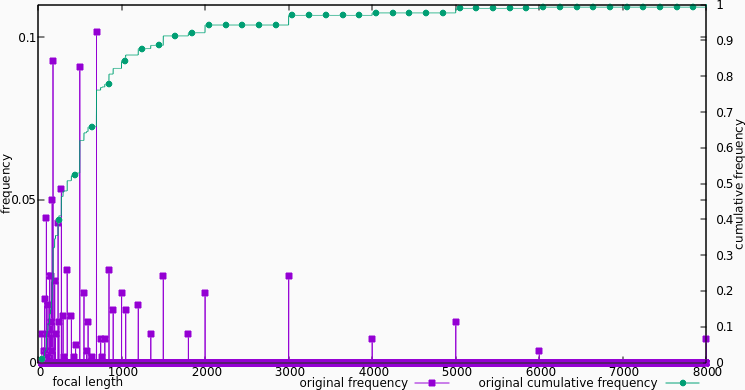
In order to understand how histogram equalization can help (and what it is), let’s take a closer look at the problem. The figure above shows the frequency and cumulative frequency of different focal lengths, normalized to 1. As you can see, most of the lenses, by far, lie in the [0, 1000] range, while the [6000, 8000] range is almost empty! Ideally, we want the cumulative frequency to be a line. That would mean the data was uniformly distributed, and thus all equal-sized segments on the slider would cover the same number of items. In the Lenshawk dataset, the cumulative frequency looks like a log curve, not a line.
The histogram equalization algorithm works as follows:
Go through the data. For each unique value, store the number of times that value occurs, divided by the size of the data set. This gives us the frequency histogram above. We can see this as a function from focal-length to the percentage of lenses with that focal length.
Go trough the histogram in order of increasing value, and store for each value the sum of the frequencies for all values smaller than or equal to the value. This gives us the cumulative frequency function as above. We can see this as a function from focal length to the percentage of lenses with that or a smaller focal length.
Scale and translate the cumulative frequencies from the [0, 1] range, to the wanted range. For contrast adjustment, it would generally be the range of possible color values in the image format. In our case, it’s the range of slider inputs, [0, 8000]. Conceptually, this gives us the same function as step 2, just with the output in a range that is more useful to us.
Normally, you would create a new data set by applying the resulting mapping to each value in the original data (normally called called back projection). For images, the value of each pixel in the resulting image would then be proportional to the percentage of pixels with a value less than or equal to that of the pixel in that same position in the original image. In other words; the new pixel values correspond to their placement in the original distribution of pixel values!
For slider scaling however, we simply pretend that our slider is the new data set, and then use the inverse of the mapping to get the value represented by a point on the slider!
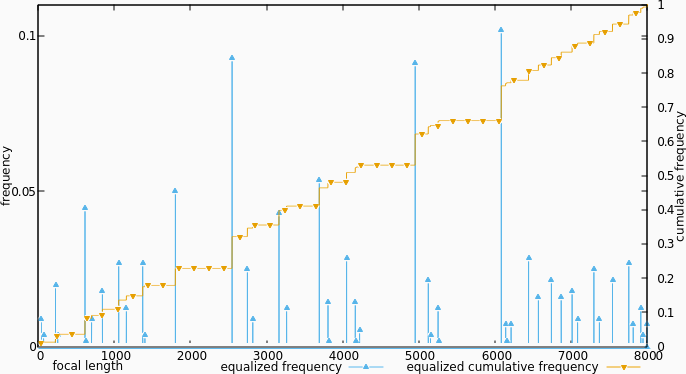
If we pretend that we did build a new data set, and then calculate the frequency histogram and cumulative frequency of it, we get the figure above. The frequencies are he exact same as before, but are distributed differently over the focal lengths (which are really slider positions now). The cumulative frequency is a lot more linear than originally.
Aftermath
Histogram equalization seems like a viable technique for creating biased slider scales. The major advantage being that the technique is general, and can be applied without manual tweaking for individual data sets; one size fits all!
Implementing histogram equalization is relatively simple, and running it relatively cheap, computationally speaking.
Interested parties can find the (mostly undocumented) source code used for this post here. I wrote the preprocessing in Gawk (A decision I thoroughly regret), but porting to other languages should be straightforward.